function approximation
write the mapping from \
usually S, Q can be continuous high-dimensional space, and even in discrete state problem. e.g. in GO game, the state space is about 10^170, to store each \
in math, this is called function approximation, it’s very intuitive idea, to fit a function from the sample points; then any point in the space, it can be represented by the function’s paramters, rather than search in all the sample points, which may be huge; and further as only the function’s parameters is required to store, rather than the whole sample points information, which is really a pleasure.
Deep Q-Learning
previously in Q-Learning, to update Q(S,A):
$ Q(S,A) <- \delta ( Q(S, A) + R + \gamma ( Q(S', A') - Q(S, A))
to approximate q(s,a) can use a neural network(NN), the benefit of NN is to approximate any function to any precise, similar to any complete orthonormal sequence, e.g. Fourier Series.
CNN approximator
the input to Q neural network is the eigenvector of state S, assuming the action set is finite. the output is action value in state-action-hyperparameter: q(s, a, \theta),
Q(S, A, \theta) ~= Q(S, A)
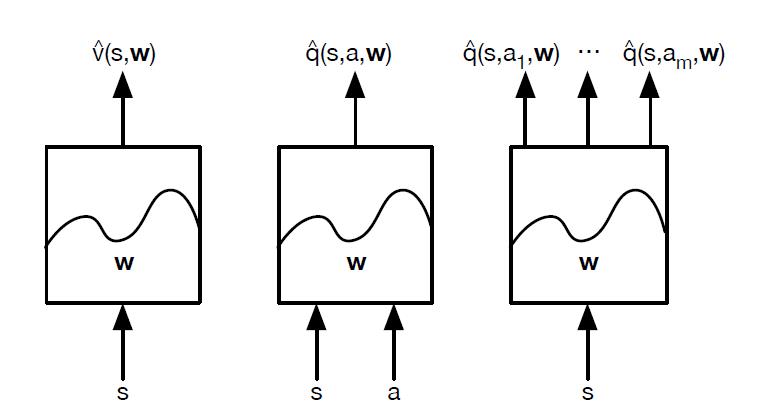
as the right most section, here assuming the action set is finite, so for each action, there is an output.
experience replay
instead of discarding experiences after one stochastic gradient descent, the agent remembers past expereicnes and learns from them repeatdely, as if the experience has happened again. this allows for greater data efficiency. another reason, as DNN is easily overfitting current episodes, once DNN is overfitted, it’s difficult to produce various experinces. so exprience replay can store experiences including state transitions, rewards, and actions, which are necessary to perform Q learning.
at time t, the agent’s experience e_t is defined as:
all of agent’s experiences at each time step over all episodes played by the agent are stored in the replay memory. actually, usually the replay memory/buffer set to some finite size limit, namely only store the recent N experiences. and then choose random samples from the replay buffer to train the network.
the key reason here is to break the correction between consecutive samples. if the CNN learned from consecutive samples of experience as they occurred sequentially in the environment, the samples are highly correlated, taking random samples from replay buffer.
target network
use a separate network to estimate the target, this target network has the same architecture as the CNN approximator but with frozen parameters. every T steps(a hyperparameter) the parameters from the Q network are copied to this target network, which leads to more stable training because it keeps the target function fixed(for a while)
go futher in DQN
Double DQN
here use two networks, the DQN network is for action selection and the target network is for target Q value generation.
the problem comes: how to be sure the best action for the next state is the action with the highest Q-value ?
Prioritized Replay DQN
Dueling DQN
yet a summary
at the begining of this series, I was thinking to make a simple summary about DQN, which looks promising in self-driving. After almost one month, there are more and more topics and great blogs jumping out, the simple idea to make a summary is not easy any more. I will stop here, and once back.